Chapter 19 第十八课(命题四十六到四十八)
第一卷结尾的三道命题都是与正方形有关的,而最重要的就是命题四十七,也就是我们熟知的勾股定理。在讲述命题四十七的时候,我们会一并补充了解中国古代里勾股定理的证明方法,看一下中西思维的异同。
19.1 命题四十六
在给定的线段上作正方形。
命题四十六这里有一个陷阱,果不其然,Alex一脚就踩下去了。因为画正方形并不是一个困难的事情,就是重复画直角和截取相等的线段即可。这里的陷阱在于,画完之后还要向读者听众证明这是个正方形。乍一看似乎有点困惑,其实是说,我们会先确定四个点和三条边,最后一条边是连接两点得到了,那么我们就需要补充证明和最后一条边有关的两个直角以及这条边与其它三条边相等的信息。如果你说你最后一条边也是通过画直角,或者作相等的线段得到的,那么你需要证明从两个底边分别作垂直的两个线段其实会重合成一条,也就是你画的这个。或者你证明从一个顶点出发,与其余三边相等的线段,这条线段的另一个端点与已知端点重合,也就是说,恰好是已知三个顶点中的另一个。怎么看后面两个证重合的论述都是要用归谬法,不免麻烦又说服力没有直接证明更有力,所以我们还是会选择连接两个端点来补齐最后一条线段,然后直接证明,即四个角均为直角,四条边均相等,那么这个图形是正方形。
这里有一个关于时刻很有意思的问题:这个正方形是在你画完线段的时候成为了一个正方形,还是在你证明完成之后成为了一个正方形?这种事实完成的时刻和论述完成的时刻,应该怎样理解呢?
在这里我希望Alex思考的是沟通的意义以及语言的价值。就好比一种药材一直在深山里,没有人告诉过采药人这其实是一种药材并且有各种神奇的功效。那么这个药材在被定义和普及之前,它并不是一个“药材”,而只是一个“植物”,你会发现,这个时候,事物是被使用者定义的,而不是由自身的存在被定义的。同样的道理,在这道题里,当绘图完成的时候,我们画了一个图形,因为它还没有被“认可”为一个正方形,而当我们证明完的时候,他才真的“是”一个正方形。(生活中学历,文凭,技能证书的意义也是这样的。)
19.2 命题四十七
在直角三角形中,直角对边上的正方形等于夹直角的两边正方形之和。
命题四十七是第一卷的最高潮部分,通过平行四边形和三角形之间的面积对应关系来完成证明。这道命题主要援引的是命题四十一和命题四十六,其中上一道命题——命题四十六基本上与最近的几道命题都不相关,可以理解为是为了命题四十七单独写出来的。而命题四十二到四十五是主要在进行再创造的工作(非构建的命题也是在为构建命题做准备)。所以其实命题四十七是证明主线上的一道题,如果将“再创造”考虑为卷一的证明中的一个分支的话。
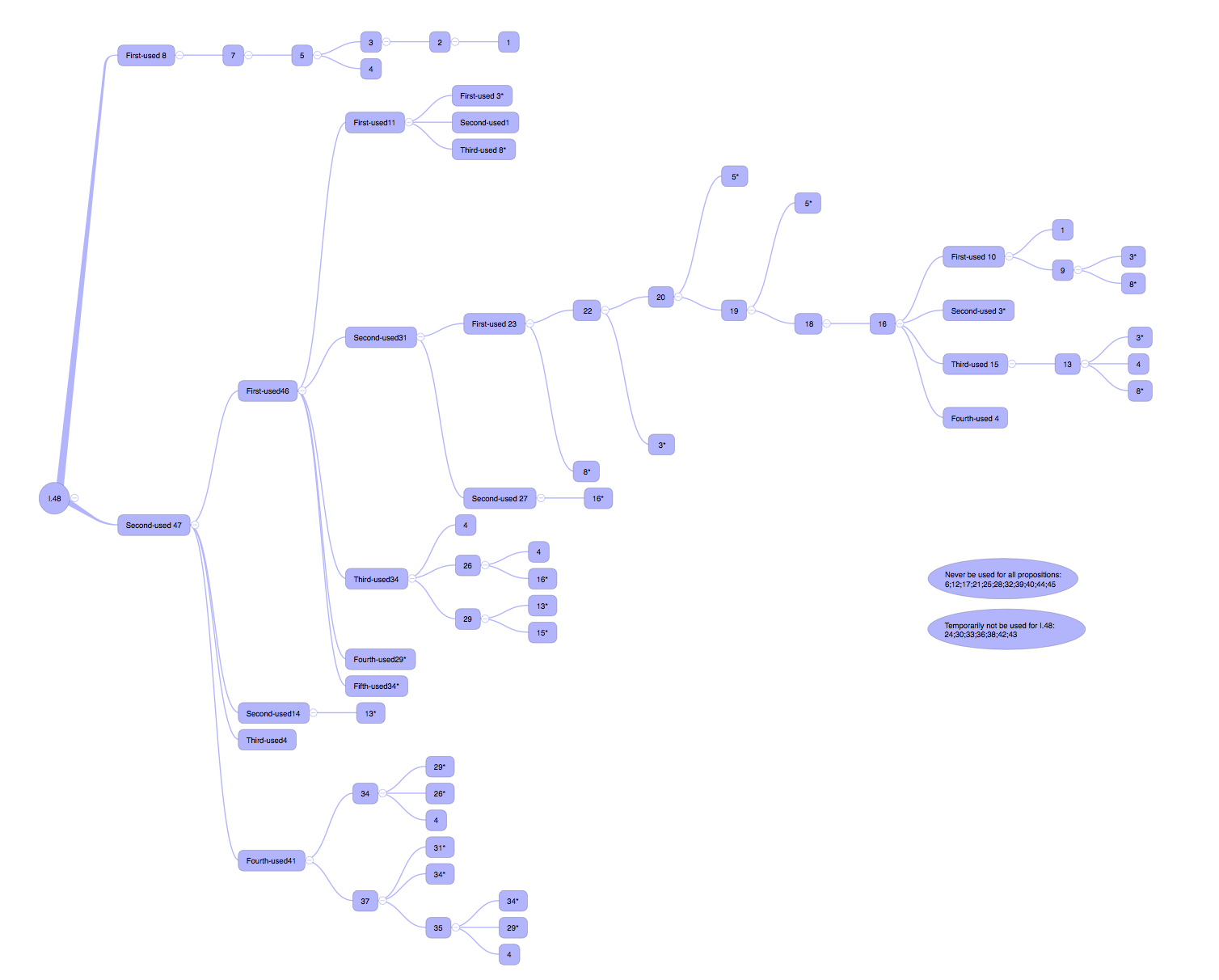
以第一卷的结尾命题48倒着通过引用的内容进行展开,可以看到逻辑发展的脉络。主线自然是最长的那一条,且这条最长的证明线的尽头是命题一。其它不同的证明线在四十七的证明中也有自己存在的目的。 做这个脉络整理的原因是想展示出西方勾股定理从零开始到证明完成中间的过程,是怎样一环扣一环推进的。而中国古代的证明方法则非常不同,以刘徽的割补术为例。割补术的特点是它从实际的角度出发,完全省略了抽象世界的构建,因此它不需要一系列证明定义的铺垫,它直接就给定图形,用拼凑的方法来证明。并且它假定了视觉认知的意义,认为可以直接认定“入”和“出”不同部分的相等性,而无需给出证明。中国古代的方法,相对而言实用性很高,易于理解,和动手能力相关。如果我们读《九章算术》就会发现,整本书从算田地的面积这种生活实用题出发,这其实会引发一个思考,西方的证明式的数学和中国古代的应用类数学,在今天都被称为数学,但是它们真的是在谈论同一个事情么???