Chapter 4 第三课（命题三）

给定两条不等线段，从长的线段中截取一条线段，使等于短的线段。

今天我们来看命题三，命题三非常短，然而今天我们讨论的内容就是如何去理解命题三的简短特征。

今天的讨论内容可以通过编程进行理解，而Alex在课外已经接触过编程，这无疑降低了理解上的难度。来看这个编程的例子。

这个例子是用编程语言C语言写的，当然我们这节课的重点不是理解这个代码的内容，而会放在格式上面，并和欧几里得的命题三进行一个类比。

首先第一行有一个include stdlib，这是说在以下的代码中会调用到stdlib这个库当中的某个功能(是malloc)，如果没有第一行的抬头，那么运行到malloc这一行代码的时候，就会报错，无法进行，因为与malloc相关的功能都无法调用。这个库对应在欧几里得的数学体系中其实就是证明之前的定义公理公设的集合，只不过C语言中有大量的定义，因为根据他们的功能性，将它们分组，只在用到的时候进行调用。

之后我们会看到四个独立的“循环”，其实前三个循环都是小循环，而最后一个char ft_split才是主循环。现在我们观察这个代码，我们会发现这个顺序是不能够改变的。因为ft_index引用了ft_definesep, 然后*ft_malloc引用了ft_definesep，最后的ft_split引用了前三者。如果改变任一顺序，代码都会报错，因为电脑线性地读取代码，如果运行到某一个”ft”，而这个”ft”在之前没有被定义，则电脑不能理解要做的内容就会报错。

欧几里得也是一样的道理，命题三之所以简短，是因为命题一二都已经提前预置好了。命题一二三放在同一页纸上，并且抬头写上包含定义公理和公设，这样才是一个可以完整运行的命题三。如果没有特意将命题一和二单独列出来，而是那么应该插入到命题三里面，参考如下：

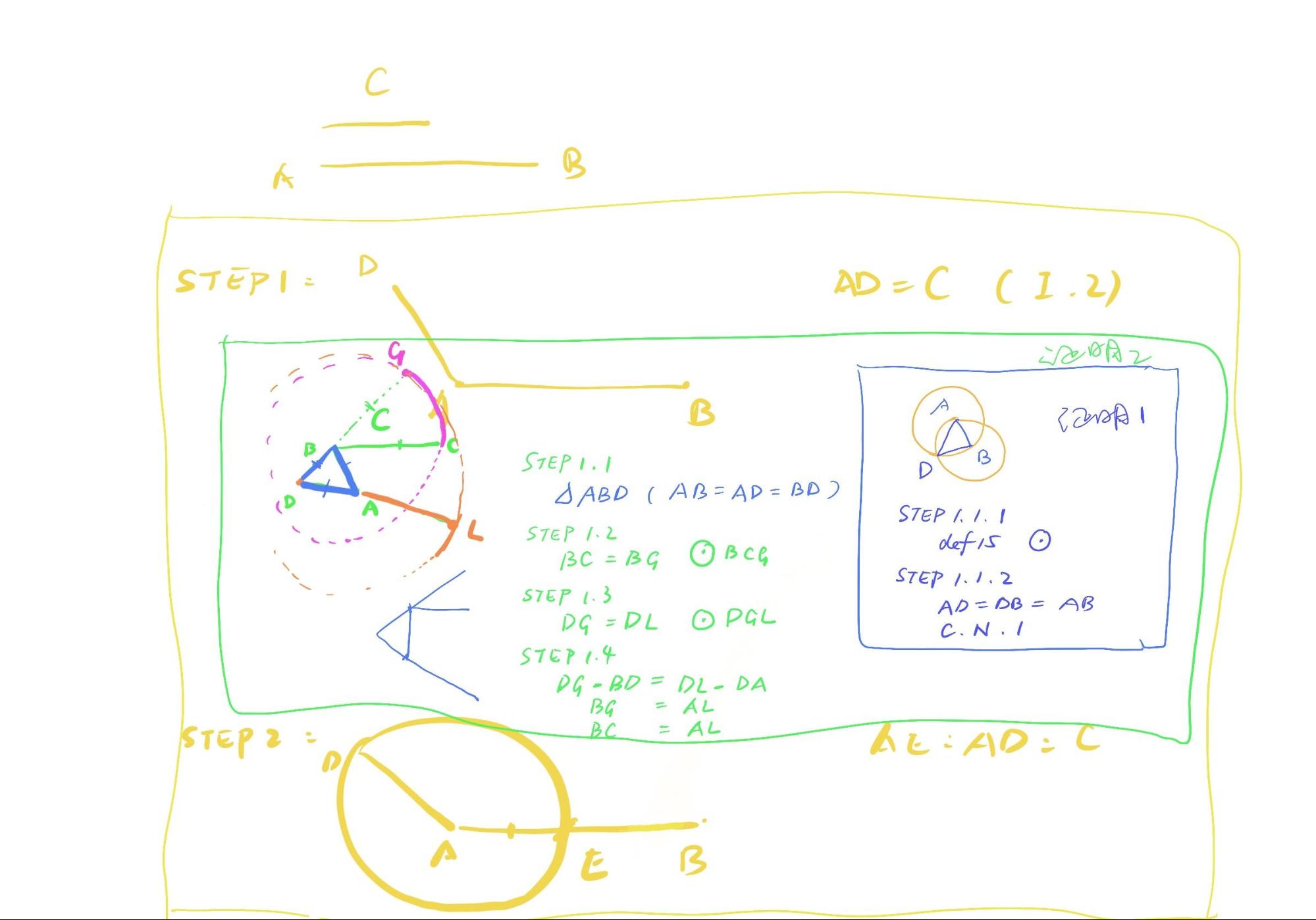
这里就会有一个很有意思的讨论，在什么样的情况下，一个模块要独立出来？这个问题等同于以下两种情况：在欧几里得的证明中，命题一和命题二为什么要单独出来呢？哪怕写进命题三里也并不会导致篇幅过长。在我们的代码案例中，为什么不能把小循环都写入大循环而是要单独出来，用的时候去调用呢。

对于会编程写代码的Alex来说，这个问题并不难理解。因为有几行代码太常用了，与其每次都要重复性的写几行，十几行，不如单独列出来，想用的时候一行命令调用即可。在欧几里得的命题证明中也是这个原则，如果我们判断一个某一个部分会经常被用到，那么我们就需要这个部分以先置命题的形式写出来，以方便后续的使用。欧几里得的《几何原本》这本书甚至可以被视为一本最初的编程代码全集。想想手动写几万行代码，全凭记忆调用各个命题，是不是就更能理解这本书对于那时时代的一个超越性？

下节课开始讲命题四，而命题1-3与命题四有一个很重要的区别。那就是前三道命题其实都是在“作图”、“绘制”，画三角形，画某个线段，截取某个线段。而命题四开始才是证明，那么下节课我们就来一起看欧几里得是怎么通过逻辑来证明事物的。

参考作业：

在日常工作中，有哪些可以提前进行的“分组”性质活动可以帮助到我们？
(这个问题的目的是引导学生思考他们的日常工作并提高其效率。例子。准备一周的衣服，以节省早上挑选的时间，买一周的牛奶，而不是每天都经过杂货店。)