Chapter 4 Discussion IV (Prop4)
If two triangles have the two sides equal to two sides respectively, and have the angles contained by the equal straight lines equal, they will also have the base equal to the base, the triangle will be equal to the triangle, and the remaining angles will be equal to the remaining angles respectively, namely those which the equal sides subtend.
Today we look at a very disputable proposition together.
In the beginning of the class, Alex claims that this proposition is about congruent triangles, which he has already learned in his school math class. Alex proves in this way: because the two sides and the angles are equal, the two triangles are congruent. Then our question arises: Have you ever wondered why two triangles are congruent because two sides are equal and the angles are equal? This is one method of determining congruent triangles, yes, but how did it become a method of determination in the first place? Now we are exploring why the math textbook declares so. Math textbooks are written this way because Euclid said so and following mathematicians all agreed, but why did Euclid make this claim and how did he make it? By the same token, we can’t just believe what Euclid said simply because he is Euclid, we can’t just think it’s right because Euclid sait it. We have to look over this proof carefully as well. The special thing about Proposition 4 is that many people read this proof of the congruent triangle and think that there is something wrong with Euclid’s argument.
Alex himself, after reading the proof, asked the question that everyone would have noticed: how can Euclid put one point on top of another, and how can he ensure that the two points coincide and are equal. In the previous Common Notions, Euclid wrote Common Notion 4: Things which coincide with one another are equal to one another. This common notion 4 is not as famous as the Postulate 5, which is about parallelism. Yet it is very significant in my eyes because this common notion is a bridge to connect the real and the geometric world. Coincidence, like overlapping, is a real-world concept that is not present in the definition; we are directly carrying a concept that is common in reality, and applying it into the geometric world, and then equating it with equality. The strangeness of Proposition 4 also stems from this, it is somewhere at a state of not true not false, depicted at the junction of reality and geometry. Alex says that if it is possible to move and overlap, then it is also possible to rotate, and in the case of rotation, since it is always the same triangle, then the old and the new must be congruent. Yes, it is possible, then in this case, the previous common notions should include overlap and it is also necessary to describe the nature of rotation. What’s more Alex mentions the use of a ruler and a protractor. However, if the rotation is still at the junction of those two worlds that are not true not false, then taking a ruler and a protractor is standing fully in the real world and thus it’s not the same.
It’s also worthy to note the logical progression of this proof. The proof itself is divided into two parts: the side by side proof of congruence; and the congruence proof of equality of the remaining sides and angles. The second part is often ignored because people subconsciously believe that two triangles are congruent, then the remaining sides and angles are equal, but in fact there is a step in between. That is, because the triangles are congruent, the remaining sides and angles are also congruent, so they are equal. This equality is not directly derived from the congruence of the triangles, but also uses the concept of the coincidence in Common notions 4.
In addition, this proof is only about the congruence of the “side-angle-side”, and does not involve the rest of the proof of congruence, such as the “side-side-angle”or “side-side-side”. Thus pay attention that the rest of the methods still need to be proved before being used.
At this point, with Alex, we also discussed why school math classes and textbooks mainly focus on theorems and properties rather than proofs. In fact, for me it is an efficiency issue. From ancient times to the present, mathematicians have kept developing the subject and have written a great amount of books, all of which are the content of everyone’s lifetime thinking, and the development to today, while we enjoy the fruits of our predecessors’ efforts, there is also a problem that we have to understand and absorb all these contents in a very short period of time, in order to continue the development. This then requires that the learning content be refined and compressed. That is, to inform the widely accepted basic proofs as ‘definitions’. Then you don’t need to know how our predecessors proved it, but only need to use it as a ‘definition’, because others have already proven him right for you. But there is also a disadvantage that it creates an impression on everyone that things can be used directly, and things are what they are. Actually, no, these properties and theorems were also proven in the beginning. For example, that two lines are parallel and congruent angles are equal is Proposition XXVIII. I told Alex that I hope he would think more when learning mathematics, and have a skeptical attitude, even though 99.99% of what is in the textbook is correct without proof, but this skeptical attitude can keep your mind sharp, observe more, and think more often.
Immediately, for proposition IV, is it always true that two congruent triangles are equal to each other? Alex soon realized that this is absolutely true, but because this is plane geometry, it looks different on a curved surface, and Alex drew this example (illustration), which is the origin of non-Euclidean geometry. He figured out this by himself and I am so proud of him.
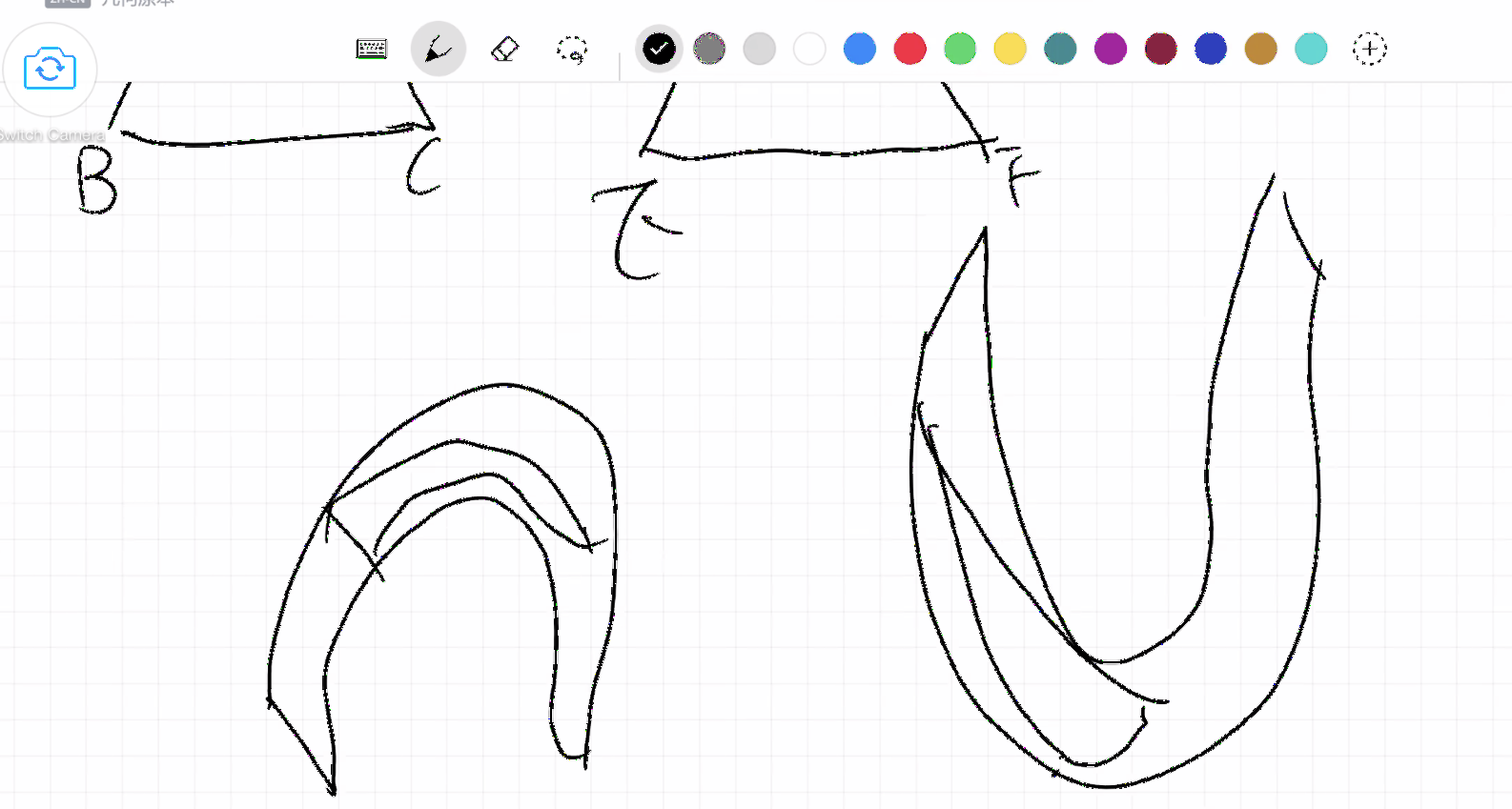
For my observation, in the argument of this lesson, Alex’s way of expression involves a very interesting issue, namely, the three incomplete expressions of mathematics: one is a literal description; the second one is symbol and letter; and the third is image. I asked Alex if he found it fun, in terms of what mathematics really is. It seems that mathematics is something that can be expressed in at least three ways. But the mathematics expressed in all three ways seems to be incomplete. We left this doubt and took our time to think about it.
At the end of this lesson, Alex took the initiative to think about and propose a way to proceed in the lesson: Alex would have to prepare the proofs before the lesson, and at the beginning of each lesson, I would dictate the proposition and Alex would draw the diagram and argue the proposition himself, either on his own or using Euclid’s method. When preparing for class, always look at Euclid’s method, and if it is different from his own, think about what is different and why Euclid used it.
Open assignments: - Keep this question open in mind: Is math created or discovered, why? - Find an example of a math equation expressed by symbols, use images/real products to describe it, use numbers to apply this principle. Which way do you feel more comfortable with? - Looking at your own example, or take “a+b, 1+1, one apple and one orange”, for you, which looks more natural to you, and why? Does this tell you something about the source of math?